15. Моделирование структуры. Основные понятия теории графов
К списку вопросов
Математическим аппаратом для моделирования структуры системы является теория графов.
Графом называется совокупность элементов и попарных связей между ними. Обозначение: G.
Элементы графа называют вершинами (V - множество вершин), а связи между ними - ребрами (E - множество ребер).
Граф, в котором хотя бы одна пара вершин соединена более, чем одним ребром, называется мульти графом;

если в какой-либо вершине петля - псевдограф.

Граф, не являющийся мульти- и (или) псевдографом - простой граф.
Кортежное определение графа: G = (V, E)
U,V,W... - вершины (U,W);
(U,V) ... – ребра. Графы можно описывать не только графически, но и в матричном виде.
Матрицей смежности графа G с множеством вершин V={V1, V2, ..., Vn} называется квадратная матрица А= ||aij||nxn, в которой aij равно числу ребер, инцидентных вершинам Vi и Vj

Матрицей инциденции простого графа G с множеством вершин V = {V1, V2, ..., Vn} и множеством ребер E = {e1, e2, ..., em} называется матрица B = ||bij||mxn, у которой bij = 1, если вершина Vj инцидентна ребру ei, и нулю в противном случае.
Степенью вершины называется число инцидентных ей ребер.
Вершина степени 0 – изолированная, а степени 1 – висячей.
Обозн.: p(V).
Дополнением графа G называется простой граф с множеством вершин V(G), в котором две вершины смежные тогда и только тогда, когда они не смежные в графе G.

Граф называется связным, если его нельзя представить в виде объединения двух графов и несвязным в противном случае. Связный регулярный граф степени 2 называется циклом.
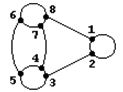
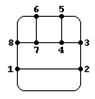
G1 и G2 называются изоморфными, если существует взаимнооднозначное соответствие между множествами их вершин, обладающее тем свойством, что число ребер, соединяющих две любые вершины в G1, равно числу ребер, соединяющих соответствующие вершины в G2.
К списку вопросов





