17. Алгоритм Флери отыскания эйлеровой линии
К списку вопросов
1736 г. Опубликовал задачу, кот получила название «Задача о Кенигсбергских мостах» с решение родилась теория графов.
Город Кенигсберг расположен на берегах реки Прегель и двух островах. Различные части города соединены 7 мостами.
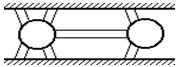
По воскресеньям граждане совершают прогулки по городу. Вопрос заключается в том, можно ли совершить прогулку таким образом, чтобы, выйдя из дома, вернуться обратно, пройдя в точности один раз по каждому мосту.
Для данного графа нельзя пройти по всем ребрам и вернуться в изначальную вершину.
Замкнутая цепь, содержащая все ребра графа, называется Эйлеровой линией; а граф, обладающий такой линией, называют Эйлеровым графом.
Если снять ограничение на замкнутость цепи, то граф называется полу-Эйлеровым.
Теорема о необходимом и достаточном условии Эйлеровости графа:
- Связный граф является Эйлеровым тогда и только тогда, когда степень каждой его вершины четная.
- Полу-Эйлеровый граф должен иметь не более двух вершин с нечетными степенями.
Алгоритм Флёри отыскания Эйлеровой линии.
Пусть G - Эйлеров граф, тогда следующая процедура всегда возможна и приводит к Эйлеровой линии графа.
Выходим из произвольной вершины и идём по ребрам графа произвольным образом, соблюдая лишь следующие правила:
1.стираем ребра по мере их прохождения и стираем также изолированные вершины, которые при этом образуются.
2.на каждом шаге идём по мосту тогда и только тогда, когда нет других возможностей.
Если не настаивать на требовании замкнутости линии, все остальное сохранить, то речь идет о плуэйлеровой линии (соответственно о полуэйлеровом графе).
Пример:
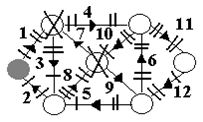
Эйлерова линия {1,3,8,7,4,10,9,6,11,12,5,2}
К списку вопросов

