20. Цикломатическое число (циклический ранг) графа. Помеченные и непомеченные деревья. Проблема перечисления деревьев
К списку вопросов
Наименьшее число ребер, которое надо удалить из данного связного графа, чтобы в нем не осталось ни одного цикла, называется цикломатическим числом или циклическим рангом графа.
Обозн.: g
g = m-(n-1)
Дерево оставшееся после удаления всех ребер, входящих в цикл называется остовым деревом(остовом).
Остовое дерево к – компонент, g=m-n+k
Для дерева g=0.
Для полного графа Rn g=(n-1)(n-2)/2
Для любого простого графа 0<=g<=(n-1)(n-2)/2
Способы построения деревьев.
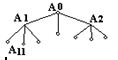
Имея n вершин построить дерево. Ответ зависит от того какими деревьями имеем дело: с помеченными или непомеченными.
Помеченный граф - граф, каждая вершина которого имеет уникальную метку от 1 до n.
Для n=3:помеченные (3), не помеченные (1)
Для n=4:помеченные (16), не помеченные (2)
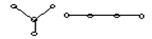
pmax=3,(4) pmax=2(12)
Для подсчета числа помеченных деревьев существует формула Кэли:
Тn = n n-2
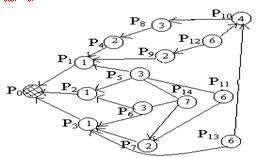
Очередность выполнения работ:
1. P14
2. P11, P12, P13
3. P10
4. P5, P6, P8
5. P4, P7, P9
6. P1, P2, P3
7. P0
К сожалению формулы, для числа непомеченных деревьев, как функции от количества вершин не найдено.
Помеченный граф – это такой граф, кажд. вершина кот. имеет свою уник. метку.
К списку вопросов


