24. Ориентированные графы. Основные определения: основание орграфа, изоморфизм, матрица смежностей, сильная связность. Ориентируемость графа.
К списку вопросов
Орграфом D называется пара (V, A); где V- непустое конечное множество элементов, называемых вершинами, A- конечное семейство упорядоченных пар элементов из V, называемых ребрами (дугами).
Пример:
Граф, полученный из орграфа удалением стрелок, называется основанием графа D. Для приведенного примера:
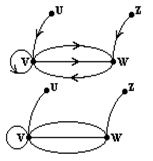
Два орграфа называются изоморфными, если существует изоморфизм между их основаниями, сохраняющий порядок вершин на каждом ребре. Матрица смежности для орграфа будет, вообще говоря, несимметричной.
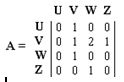
В матрице смежности орграфа в клетке (u, v) ставится 1, если из u в v и ставится 0, если из v в u.
Построим матрицу смежности для графа D.
Существуют также понятия орцепи и орцикла.
Пример орцепи: Z-W-V-W
Орграф называется сильно связным, если существует простая цепь из V в W для любой пары его вершин V и W.
Пример сильно связного орграфа:
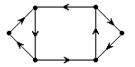
Граф G будем называть ориентируемым, если каждое его ребро может быть упорядочено таким образом, что полученный в результате орграф будет сильно связным.
Теорема Робинсона (необходимое и достаточное условие ориентированности графа): Пусть G - связный граф. Он ориентируем тогда и только тогда, когда каждое его ребро содержится, по крайней мере в одном цикле.
Легко видеть, например, что любой Эйлеров граф ориентируем, поскольку достаточно по любой Эйлеровой линии, ориентируя ребра в направлении движения по ним.
Если речь идет о транспортной сети, тогда если движения всюду двустороннее, то возможность приехать из одной части города в другую обеспечивается связанностью графов, если движение по всем улицам одностороннее, то та же возможность обеспечивается сильной связанностью графа дорог из т. Робинсона следует, что сориентировать граф всегда можно, если карта дорог не содержит «мостов» и «тупиков».
Следствие: Если граф не содержит мостов (тупиков), он ориентируем.
Связный орграф называется Эйлеровым, если в нем существует Эйлерова орцепь, т.е. замкнутая орцепь, содержащая каждую его дугу.
Назовем полустепенью исхода неP(V) любой вершины V число дуг орграфа имеющих вид (V, W). Аналогично определяем полустепень захода неP(V).
Орлемма о рукопожатиях: Сумма полустепеней захода всех вершин графа D равна сумме полустепеней исхода этих вершин.
К списку вопросов


