25. Орцепи и орциклы. Эйлеровы и гамильтоновы орграфы. Орлемма “о рукопожатиях”
К списку вопросов
Орграфом D называется пара V(D), A(D); где V(D) - непустое конечное множество элементов, называемых вершинами, A(D) - семейство упорядоченных пар элементов из V(D), называемых ребрами. Пример:
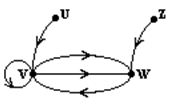
Орцепь Z=>W=>V=>W=>U. Орграфы называются сильно связными, если существует простая орцепь из V=>W для любой пары вершин V и W. Замкнутая орцепь, проходящая через все дуги орграфа - называется Эйлеровой линией. А граф, содержащий эту линию – эйлеров граф.Замкнутая простая орцепь, проходящая через все вершины – гамильтонова орлиния. А граф, обладающий такой линией называется гамильтонов орграф.
Теорема (необходимое и достаточные условия эйлеровости графов)
Связный граф является Эйлеровым, тогда и только тогда, когда каждая его вершина имеет четную степень. Оценки гамельтоновости: Теорема Дирака. Если в простом графе с числом вершин n (n>=3) ?(V)>=n/2 для любых n , то граф является гамельтоновым.
Орлемма о рукопожатиях: сумма полустепеней исхода всей сети равна сумме полустепеней захода. Полустепень захода – количество входящих стрелок (дуг). Полустепень исхода - количество выходящих стрелок (дуг). Необх. и дост. условия гамильтонового орграфа до сих пор не найдены (не существуют).
К списку вопросов
