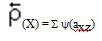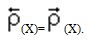29. Алгоритм отыскания максимального потока сети. Определение максимального потока сети.
К списку вопросов
Пример:
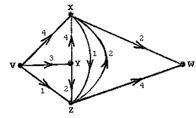
1. fu- функция, которая ставит в соответствие каждому ребру а неотрицательное действительное число fu (а), называемое его пропускной способностью.
2. полустепенью исхода вершины Х назовем сумму пропускных способностей всех дуг вида аxz.
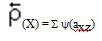
Аналогично определяем полустепень захода любой вершины Х:


3.сток - вершина, для которой P<(W)=0;
источник – P>(V)=0.
4.будем называть сетью пару (D, fu), где D - орграф, имеющий ровно один источник и один сток ; fu - функция пропускных способностей.
Обозн.: N fu = (D, fu) Для данной сети N fu определим поток ч/з сеть как функцию fi, ставящую в соответствие каждой дуге а неотрицательное действительное число fi (а), называемое потоком ч/з дугу а и, обладающее 2-мя свойствами:
1. для любой дуги а fi(а)<=fu (а);
2. для любой вершины (х,y), не совпадающей с источ. исходов, для любых х,y не равных V,W:
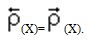
Для данной сети пропускных способностей N fu определим сеть потоков N fi =(D, fi), где fi - функция потоков. Для сетей имеет место аналог орлеммы «о рукопожатиях»: сумма полустепеней исхода всей сети равна сумме полустепеней захода. Из орлеммы «о рукопожатиях» следует, что сумма потоков ч/з дуги, инцидентные источнику, = сумме потоков ч/з дуги, инцидентные стоку. Это общая сумма называется величиной потока ч/з данную сеть. Интересующие нас потоки – это потоки, имеющие наибольшую возможную величину. Они называются максимальными потоками. В общем случае сеть может иметь несколько максимальных потоков, но их величины, естественно, должны совпадать.
К списку вопросов