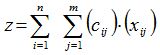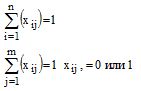30. Некоторые приложения транспортных сетей: организация оптимального грузооборота; оптимальное использование оборудования; задача “о назначениях”.
К списку вопросов
Допустим имеются станции отправления, в кот. сосредоточен груз и есть станции получения.
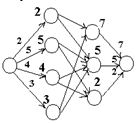
Необходимо так организовать перевозки, чтобы было перевезено максимум общего количества груза потребителям.
Примечание: в отличие от транспортной задачи в этой задаче не от каждого пункта отправления существует путь к каждому пункту назначения.
Одним из способов решения такого рода задач является сведение их к сетевым. Вводят 2 фиктивные вершины: X•- источник; Y•- фиктивный сток. Сводится к отысканию максимального потока.
- оптимальное использование оборудования
Пусть имеются станки А,B, C,D, выпускающие детали артикулов ?, ? и ?.
Каждый станок может изготавливать детали только определенных артикулов.
Производительность каждого станка при выпуске различных деталей различна и указана цифрой на соответствующей дуге.
Некоторая схема организации работ изображена на рисунке:
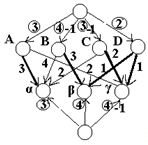
Внизу в кружочках введены потребности в деталях данного артикула в 1 времени. В самых верхних кружочках показаны производительности каждого станка, т.е. максимальное количество деталей, кот. он может выпустить в 1 времени. На рис изображена неоптимальная схема загрузки станков. Жирная линия означает, что станок работает на полную мощность по выпуску данного изделия. Сверху цифры со знаком «-» показывают насколько недогружены станки, а снизу такие же цифры – насколько неудовлетворенны потребности в изделиях соответствующего артикула. Задача состоит в том, чтобы найти такую оптимальную схему загрузки станков, кот. бы минимизировала недогрузку станков и недополучение требуемых деталей. Один из способов сведения данной задачи к сетевой. Вводятся фиктивный источник и сток. И рассматривая как сеть ориентированного графа, пытаемся найти максимальный поток ч/з эту сеть. Легко видеть, что эти задачи эквивалентны
- задача “о назначениях”(оптимальное трудоустройство)
Пример 1: Пусть имеется несколько кандидатов на ряд должностей.
Некоторые кандидаты имеют несколько специальностей, а некоторые должности м. б. заняты не одним, а несколькими кандидатами.
Если рассмотреть кандидатов на должности «на глазок», то не исключено, что некоторые должности оказываются не замещенными, а некоторых кандидатов придется отправить домой.
Найти такое назначение кандидатов на должность (оптимальное), чтобы минимизировать количество не заполненных вакансий, а с другой стороны неустраиваемых кандидатов.
Пример 2: Рассмотрим случай, когда требуется распределить m работ (или исполнителей) по n станкам. Работа i (=1, 2 ...m) выполнимая на станке j (=1, 2 ...n) связана с затратами cij .
Задача состоит в том, чтобы распределить работы по станкам так, чтобы это соответствовало минимуму суммарных затрат. Такая задача известна как задача о назначениях.
Ее можно рассматривать как частный случай транспортной задачи. Работы - исходные пункты, станки - пункты назначения. Предложение и спрос в каждом пункте равны 1, то есть ai = 1 для всех i и bj = 1, для всех j.
Стоимость "прикрепления" равна cij. Если какую-либо работу нельзя выполнить на каком-либо станке, то стоимость cij берется равной очень большому числу М.
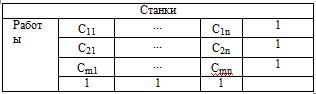
Задачу о назначениях можно представить следующим образом:
Xij = { 0, если j- ая работа не выполняется на i - ом станке; 1, если выполняется.
Тогда
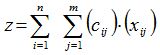
при ограничениях
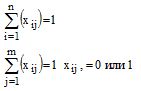
Прежде чем решать задачу о назначениях получим опорное решение. Оно будет вырожденным.
Эта особенность характерна для задачи о назначениях независимо от метода нахождения опорного плана.
Для задачи о назначениях был разработан специфический метод решения.
Оптимальное решение задачи о назначениях не изменится, если к любой строке или столбцу матрицы стоимостей прибавить (вычесть) одну и ту же величину.
Это соображение показывает, что если можно построить новую cij1 - матрицу с нулевыми элементами и эти нулевые элементы или их подмножество соответствуют допустимому решению, то такое решение будет оптимальным, так как стоимость не может быть отрицательной.
Дальнейшая процедура состоит в проведении минимального числа прямых через строки и столбцы, чтобы все нулевые элементы оказались вычеркнутыми. Выбирается наименьший невычеркнутый элемент.
Этот элемент вычитается из каждого невычеркнутого и прибавляется к каждому элементу, стоящему на пересечении проведенных прямых.
К списку вопросов