35. Оценка числовых характеристик случайных величин и вероятностей событий методом Монте- Карло
К списку вопросов
Метод Монте-Карло состоит в решении различных задач вычислительной математики и анализа сложных систем путем построения для каждой задачи случайного процесса с параметрами приближенно равными искомым величинам этой задачи.
При этом определение искомых величин происходит путем наблюдения за случайным процессом и вычисление его статистических характеристик, приближенно равных искомым параметрам.
Оценка некоторого параметра.
х - искомый параметр
Е- случайная величина такая, что М(?) = х
Генерируем n реализаций ? и находим их среднее значение:

При достаточно большом n:

Теория о равномерном распределнии:

Рассмотрим закон равномерной плотности (равномерное распределение).
Е - случайная величина подчинена ЗРП, если её функция распределения задается формулой:

Отметим одно важное свойство ЗРП.

Для любого интервала (a,b), целиком принадлежащего [0;1] вероятность попадания ррсв внутрь интервала (a,b) равна длине этого интервала и не зависит от расположения (a,b) на отрезке [0;1].
Производится опыт, в котором может произойти некоторое событие А с вероятностью Р.
Сгенерируем n реализаций равномерно распределенной в [0;1] случайной величины:

В массив H записываем 1, если ?iP.
Пусть m - количество единиц в массиве H, тогда

при достаточно большом n (основано на ЗБЧ в форме Бернулли).
Оценка вероятности полной группы несовместных событий.
Производится серия опытов, в каждом из которых может появиться одно из k несовместных событий А1, А2, ..., Аk с вероятностями Р1, Р2, ..., Рk соответственно.
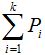
для полной группы несовместных событий.
Сгенерируем n реализаций случайной величины ?. Если
?iР1и т.д.
Обозначим mi - количество чисел i в массиве H. Тогда

Оценка вероятности сложных событий.
n испытаний Бернулли с вероятностью успеха P (n=50)
m - число успехов.

Если 0q>30, то в массив Q заносим 1 ; q<=30, то в Q заносим 0
L - количество единиц в Q.

К списку вопросов